Aizawa Attractor

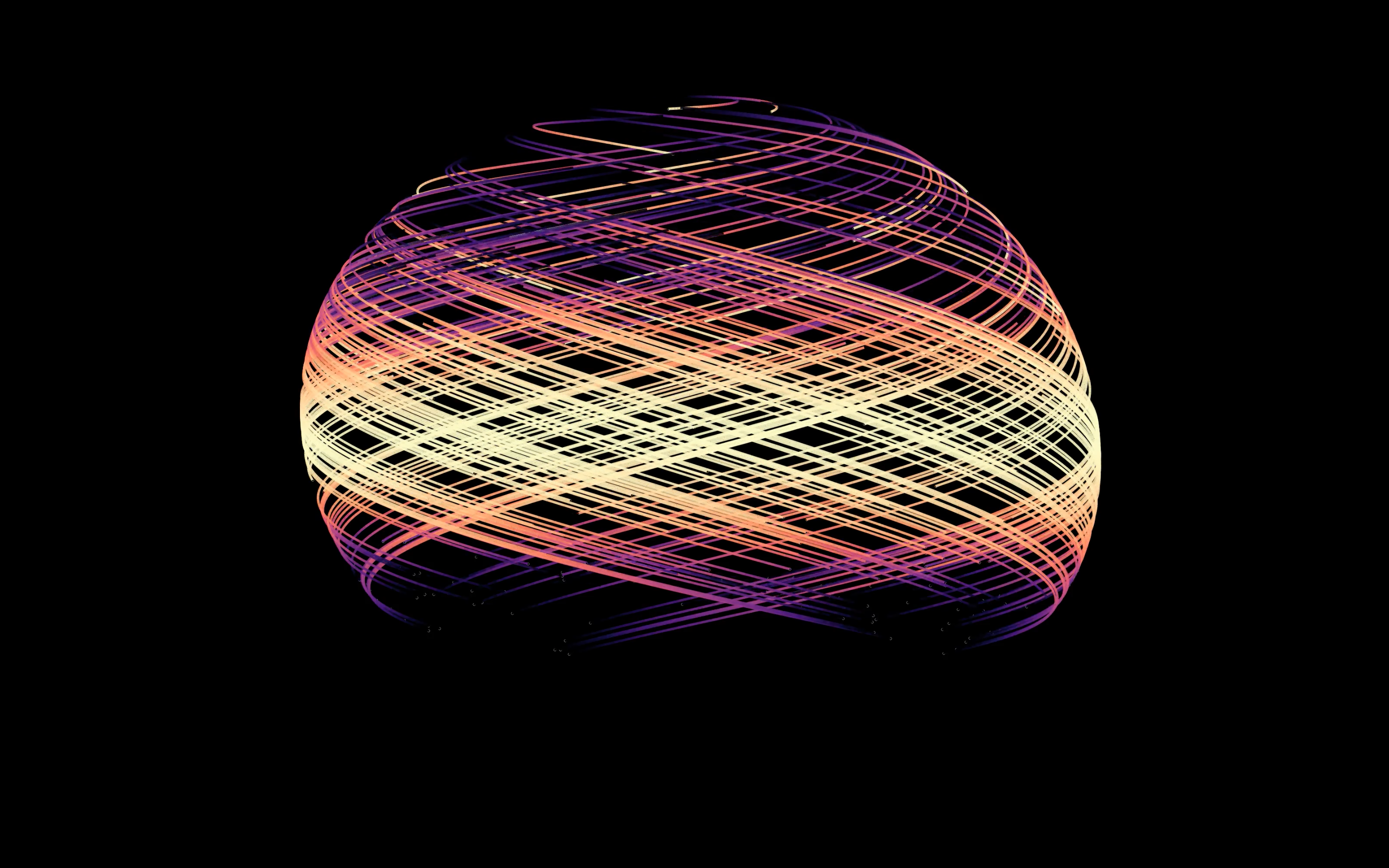
Overview

The Aizawa attractor is a visually dense and geometrically elegant system discovered in the study of nonlinear dynamics and strange attractors. It was introduced by Yoshisuke Aizawa and is notable for producing toroidal and layered forms in phase space. The system is designed with additional symmetry and radial behavior compared to more classical chaotic systems. Instead of sharp scrolls or folding loops, the Aizawa attractor creates a structure that appears spherical and pulsating, with motion expanding and contracting in a rhythm that seems almost orbital. The motion remains chaotic, but its path suggests cohesion and containment, forming a complex object that looks almost like a woven shell or energy field.

The Aizawa system is described by the following differential equations:

dx/dt = (z − b)·x − d·y
dy/dt = d·x + (z − b)·y
dz/dt = c + a·z − (z³ / 3) − (x² + y²)(1 + e·z) + f·z·x³

The system has six parameters: a, b, c, d, e, and f. A common set of values that generates the attractor's characteristic form is a = 0.95, b = 0.7, c = 0.6, d = 3.5, e = 0.25, and f = 0.1. These equations combine polynomial and trigonometric-like behaviors with nonlinear coupling, resulting in a continuous but never-repeating flow through three-dimensional space. The attractor remains bounded and fills out a central spherical region, forming layer after layer as it evolves.

To simulate the Aizawa attractor, I applied the Euler method to integrate the equations forward in time. Starting from an initial state, the derivatives were calculated at each step based on the current coordinates and parameters. These derivatives were used to update the position, allowing the trajectory to unfold iteratively. The system's complexity comes not just from chaotic divergence, but from the delicate interplay between radial and angular motion. The terms involving x², y², and z³ introduce a kind of pulsation, pulling the trajectory inward and pushing it outward in an ongoing cycle.

Visually, the attractor appears as a glowing structure with hundreds of intertwined lines forming a tight spherical weave. I assigned color gradients based on time to accentuate motion and depth. The final render shows a shape that is both organic and constructed, with repeated intersections that never quite overlap. The Aizawa attractor invites the viewer into a space that feels alive, pulsing with mathematical rhythm. It is not a system that spirals or scrolls outward, but one that folds in on itself, building its form from layers of motion, encoding complexity in the geometry of repetition without repetition.

You can find my code repository here.