Chen Attractor

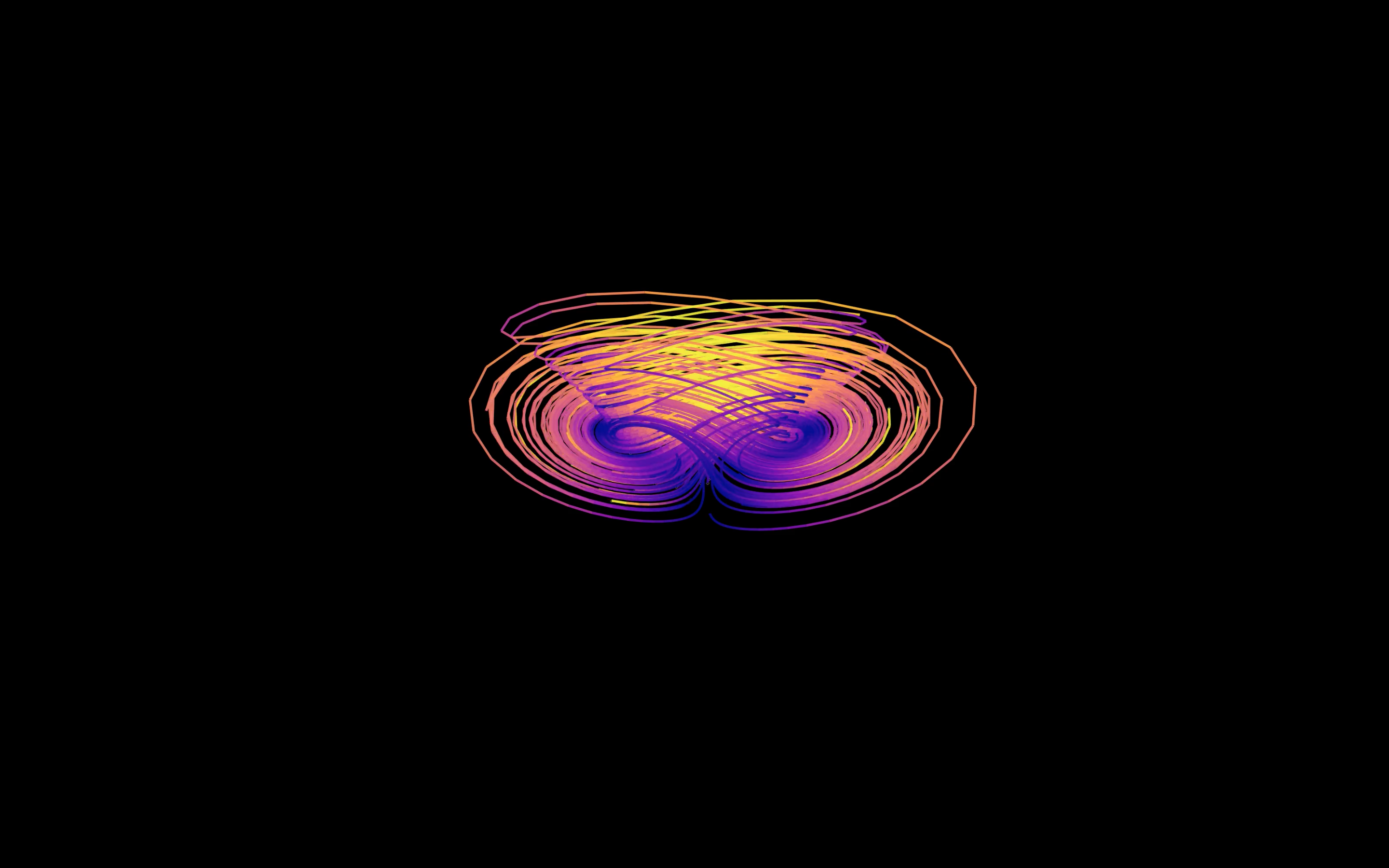
Overview

The Chen attractor is a well-known example of a chaotic dynamical system discovered by Guanrong Chen in 1999. It belongs to a distinct class of three-dimensional continuous-time systems and is defined by a set of nonlinear differential equations that generate a complex, bounded, and non-repeating trajectory in phase space. The attractor is often described as a double scroll due to its twin-lobed geometry, where the path oscillates unpredictably between two opposing regions. Like other strange attractors in chaos theory, the Chen system is highly sensitive to initial conditions. Even a tiny variation in starting position can result in a completely different path, yet all trajectories remain confined within a well-defined volume.

The Chen system is governed by the following equations:

dx/dt = a(y − x)
dy/dt = (c − a)x − xz + cy
dz/dt = xy − bz

The parameters a, b, and c determine the system’s behavior. A common choice that produces chaotic motion is a = 35, b = 3, and c = 28. These equations describe how a point in space evolves over time, with each component influenced by a nonlinear interaction between the others. The resulting trajectory does not repeat or stabilize but instead folds and stretches through space, forming a shape that reveals the delicate interplay between order and instability. The geometry of the Chen attractor contains rotational symmetry and internal layering, with each turn of the scroll exposing the recursive behavior embedded in the system.

To simulate this system, I implemented the equations in Python using the Euler method for numerical integration. Starting from a given initial point, I repeatedly applied the Chen equations to compute the rate of change at each step, then advanced the system forward using a fixed time increment. This produces a sequence of coordinates that trace the attractor’s evolution over time. Each point is the result of applying the system’s rules precisely, yet the overall shape cannot be predicted from any one segment alone. It is only through iteration that the scrolls begin to form and the hidden structure of the attractor is revealed.

The final output consists of thousands of connected points, forming a thread that oscillates between two spiral regions. Slight differences in initial conditions result in dramatically different outcomes, yet all trajectories fill the same volume with dense, non-intersecting lines. I used multiple trajectories and colored them based on time to highlight the flow and emphasize the movement between the scrolls. What emerges is not just a visual artifact but a direct consequence of the Chen equations. The attractor exists not in any one frame, but in the continuous unfolding of the system’s dynamics, creating a shape that embodies the mathematical essence of chaos.

You can find my code repository here.