Fibonacci Spiral

Overview

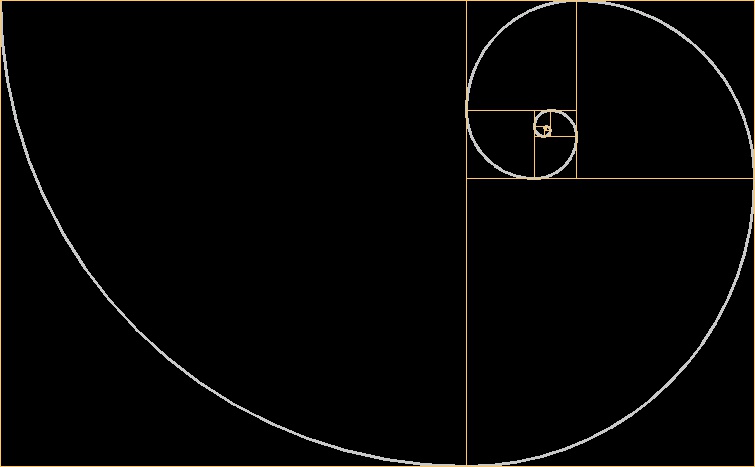
The Fibonacci spiral is a geometric approximation of the golden spiral, constructed by arranging squares whose side lengths follow the Fibonacci sequence. Each successive square grows in size according to the recursive rule Fn = Fn−1 + Fn−2, and when quarter circles are drawn through each square, they approximate a continuous spiral. Although this construction is not a true logarithmic spiral, the ratio between consecutive Fibonacci numbers converges to the golden ratio φ, so the resulting shape becomes increasingly close to the golden spiral as more squares are added. The curve captures the essence of self-similarity and recursive growth found in natural patterns, such as the arrangements of seeds, shells, and branching systems.

To generate this spiral, I implemented an algorithm that first builds the underlying sequence and then arranges each square in a way that respects rotational alignment. At each step, I calculated the position and orientation of the next square by updating the direction vector and appending the quarter arc connecting the new square. The spiral was then traced by combining these arcs into a continuous path. I used careful geometric transformations to preserve the structure and curvature across the entire figure. The final render demonstrates how a simple numerical rule gives rise to a visually harmonic structure, rooted in recurrence but expressed through spatial proportion.

You can find my code repository here.