Trapped Knight Sequence Path

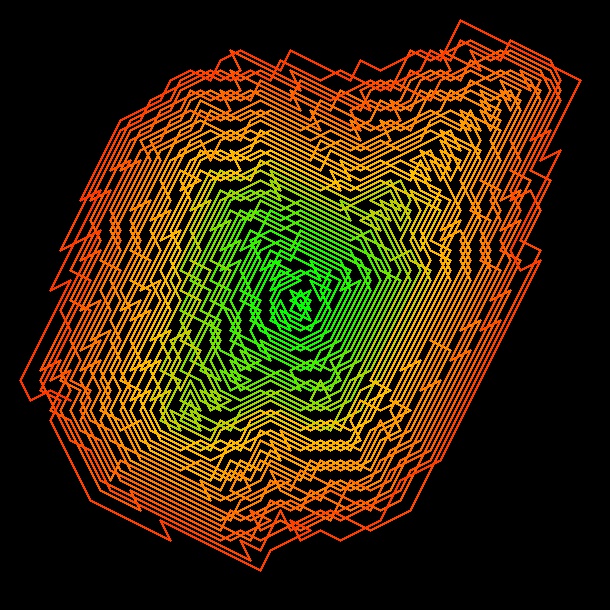
Overview

This figure is based on a knight’s journey across an infinite chessboard where each square is numbered spirally outward from the center. The knight begins on square one and is forced to move by a strict rule: it may only jump to the smallest unvisited number available from its legal knight moves. What unfolds is a sequence not of random motion but of deterministic exploration, tracing a vibrant, curling path that grows ever more complex before halting forever. Like a prisoner sealed within its own decisions, the knight becomes completely trapped after 2016 steps, surrounded on all sides by already visited squares, ending its journey on square 2084.

The mathematics behind the movement lies in a clever intertwining of geometry and number theory. The spiral grid assigns integer values to positions on an expanding square shell while the knight’s L-shaped movement enforces a rigid constraint on traversal. This creates natural bottlenecks, turns, and surprising symmetry. The rule that selects the lowest reachable unvisited number at each step ensures the path always takes the seemingly most conservative route forward, leading paradoxically to a self-made trap. The sequence produced is finite but rich with structure, and the positions not visited form another infinite sequence of their own.

In the code implementation a matrix stores the numbered grid while the knight’s current location is updated after each valid move. At every step the eight possible knight jumps are scanned for reachable coordinates, and the one corresponding to the smallest unused number is selected. The color progression across the plotted path reflects the step count, producing a glowing spiral of motion that burns from green to red. This is not a random walk, it is a deterministic journey through space shaped entirely by minimal choice and self-limiting logic.

You can find my code repository here.